Apriori Algorithm

Apriori Algorithm Overview

The Apriori algorithm is one of the most well-known algorithms for association rule mining and frequent itemset discovery.

Key Concepts

• Frequent Itemset: A set of items that appears together in transactions above a minimum support threshold
• Support: The frequency of occurrence of an itemset in the database
• Confidence: The probability that a rule is correct

Algorithm Steps

1. Generate 1-itemsets: Find all frequent 1-itemsets (single items)
2. Generate k-itemsets: For k ≥ 2, generate candidate k-itemsets from frequent (k-1)-itemsets
3. Prune candidates: Remove candidates that have infrequent subsets (Apriori property)
4. Count support: Scan database to count support for remaining candidates
5. Filter frequent: Keep only itemsets meeting minimum support threshold
6. Repeat: Continue until no more frequent itemsets can be generated

The Apriori Property

Any subset of a frequent itemset must also be frequent.

This property allows us to prune candidate itemsets efficiently.

Pseudocode

L₁ = {frequent 1-itemsets}
for (k = 2; L_{k-1} ≠ ∅; k++) {
    C_k = generate_candidates(L_{k-1})
    for each transaction t in database {
        C_t = subset(C_k, t)
        for each candidate c in C_t {
            c.count++
        }
    }
    L_k = {c ∈ C_k | c.count ≥ min_support}
}
return ∪_k L_k

Complexity

• Time Complexity: O(2^n) in worst case, where n is the number of items
• Space Complexity: O(2^n) for storing all candidate itemsets

Limitations

• Multiple database scans required
• Large number of candidate itemsets generated
• Memory-intensive for large datasets
• Performance degrades with increasing number of items

Experimental Results

Our implementation includes comprehensive runtime tracking and visualization. See the Results page for detailed performance analysis and comparison with FP-Growth.

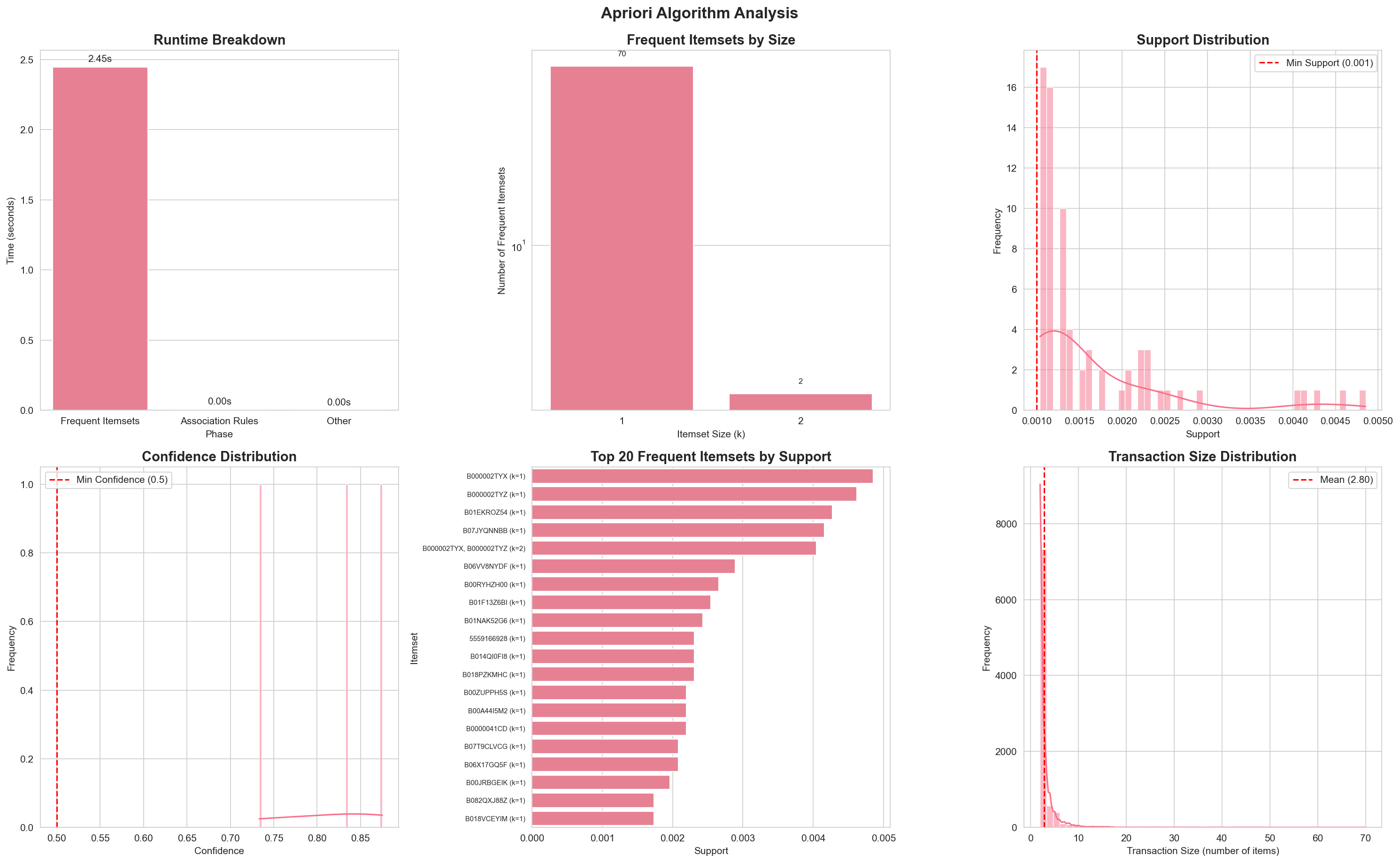
Complete analysis visualization showing runtime breakdown, frequent itemsets by size, support and confidence distributions, top itemsets, and transaction size distribution.

Related Algorithms

The FP-Growth algorithm addresses many of Apriori’s limitations by using a tree-based approach that avoids candidate generation. See the FP-Growth Algorithm page for details on this alternative approach.