FP-Growth Algorithm

FP-Growth Algorithm Overview

The FP-Growth (Frequent Pattern Growth) algorithm is an efficient alternative to the Apriori algorithm for mining frequent itemsets. It was proposed by Han et al. in 2000 and uses a tree-based data structure to compress the database representation.

Key Concepts

• FP-Tree (Frequent Pattern Tree): A compressed representation of the database that preserves frequent itemset information
• Header Table: A linked list structure that connects all nodes containing the same item
• Conditional Pattern Base: The sub-database consisting of prefix paths ending with a given item
• Conditional FP-Tree: An FP-tree built from a conditional pattern base

Algorithm Steps

1. Scan database: Count support for each item and identify frequent 1-itemsets
2. Sort items: Order items by frequency (descending) and remove infrequent items
3. Build FP-Tree: Construct the FP-tree by inserting transactions one by one
4. Mine FP-Tree: Recursively mine the FP-tree to find all frequent itemsets
   • For each item in the header table (from least frequent to most):
     • Generate conditional pattern base
     • Construct conditional FP-tree
     • Recursively mine the conditional FP-tree

Key Advantages

• No candidate generation: Unlike Apriori, FP-Growth doesn’t generate candidate itemsets
• Fewer database scans: Requires only two passes over the database
• Compact representation: FP-tree compresses the database efficiently
• Better performance: Typically faster than Apriori, especially for dense datasets

FP-Tree Construction

The FP-tree is built by:

1. Sorting items in each transaction by frequency
2. Inserting transactions as paths in the tree
3. Sharing common prefixes between transactions
4. Maintaining header tables for efficient traversal

Pseudocode

// Build FP-Tree
Scan database to find frequent 1-itemsets
Create root node of FP-tree
for each transaction T in database {
    Sort T by frequency
    Insert T into FP-tree
}

// Mine FP-Tree
function mine_fp_tree(FP-tree, min_support) {
    if FP-tree contains only one path P {
        Generate all combinations of items in P
        return combinations with support ≥ min_support
    } else {
        for each item i in header table (from bottom to top) {
            Generate pattern β = i ∪ α
            Construct β's conditional pattern base
            Construct β's conditional FP-tree
            if conditional FP-tree ≠ ∅ {
                mine_fp_tree(conditional FP-tree, min_support)
            }
        }
    }
}

Complexity

• Time Complexity: O(n × m) where n is the number of transactions and m is the average transaction length
• Space Complexity: O(n × m) for storing the FP-tree, but typically much more compact than Apriori’s candidate sets

Comparison with Apriori

Aspect	Apriori	FP-Growth
Database Scans	Multiple (k scans for k-itemsets)	Two (one for counting, one for building tree)
Candidate Generation	Yes	No
Data Structure	Hash tables / Lists	FP-Tree
Memory Usage	High (stores all candidates)	Lower (compressed tree)
Performance	Slower for dense datasets	Faster, especially for dense datasets
Scalability	Limited	Better

Limitations

• Memory overhead: FP-tree can still be large for very sparse datasets
• Tree construction: Initial FP-tree construction can be time-consuming
• Recursive mining: Recursive pattern mining can be complex to implement efficiently

Experimental Results

Our implementation demonstrates FP-Growth’s superior performance compared to Apriori. See the Results page for detailed performance analysis and comparison.

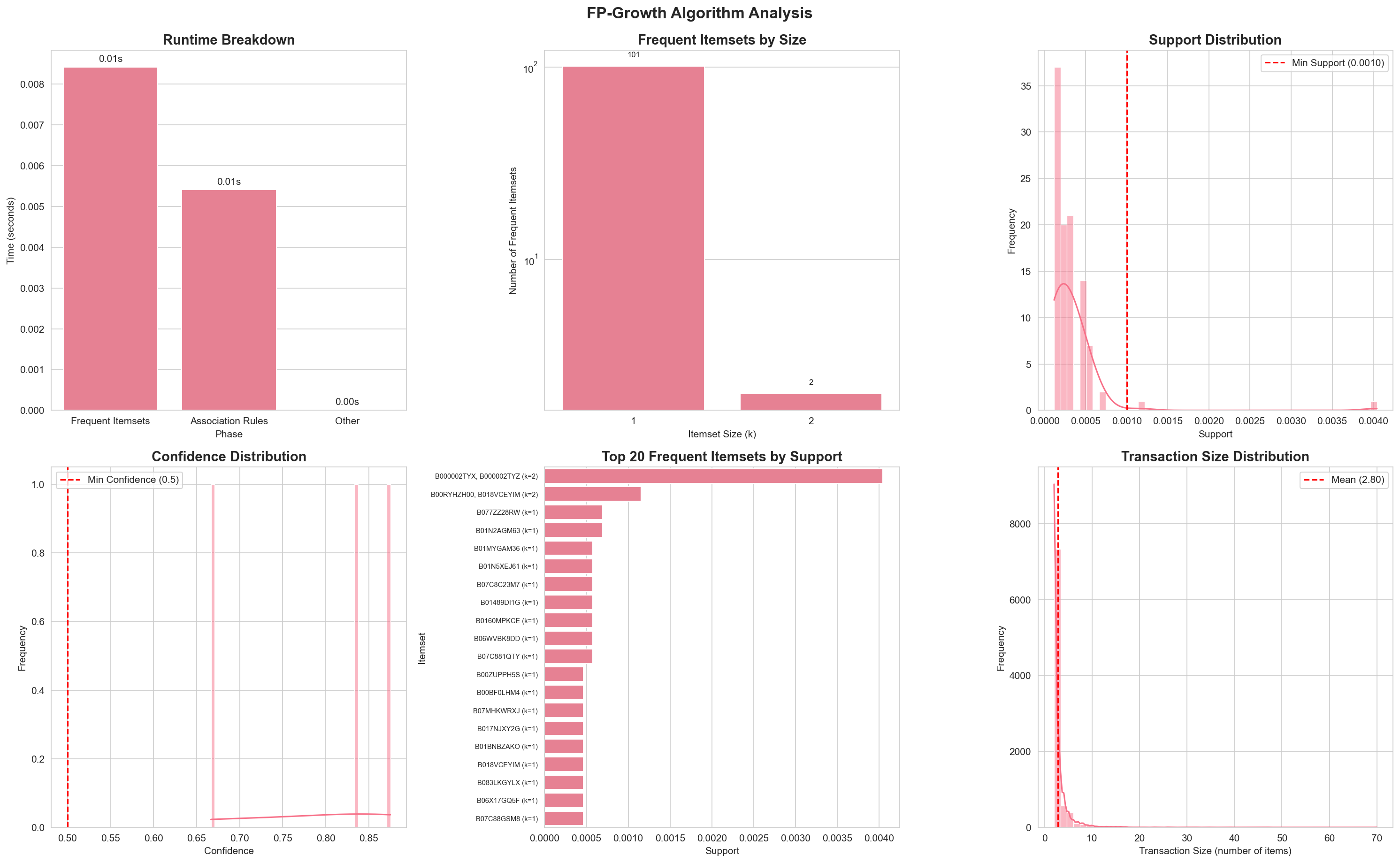
Complete analysis visualization showing runtime breakdown, frequent itemsets by size, support and confidence distributions, top itemsets, and transaction size distribution.

Relationship to Improved Apriori

While FP-Growth offers a fundamentally different approach, understanding both algorithms helps in:

• Comparing performance characteristics
• Understanding trade-offs between approaches
• Developing hybrid methods
• Applying concepts from FP-Growth to improve Apriori-based algorithms