Improved Apriori Algorithm

Overview

The Improved Apriori algorithm (also known as the Weighted Apriori Algorithm) is an optimized version of the traditional Apriori algorithm that eliminates repeated database scans by using intersection-based counting. The key innovation is calculating support for candidate itemsets by intersecting the support transactions of their K-order subsets, ensuring the database is scanned only once.

Key Innovation: Single Database Scan

The primary enhancement involves calculating the support of candidate itemsets $C_k$ based on the support transactions of their K-order subsets. This ensures the database is scanned only once, dramatically improving efficiency compared to the traditional Apriori algorithm.

Analogy: Instead of checking the entire country (database) every time a new address (candidate itemset) is generated, the algorithm cross-references existing delivery records (K-support transactions) to confirm the new address is valid, completing the task much faster.

Algorithm Description

Input

DB: Transactional Database
wminsup: Minimum Weighted Support

Output

F: The complete set of frequent patterns

Method

Initial Scan and $L_1$ Generation (Single Database Scan Phase)
- Scan DB once to find initial support transactions for all items
- Generate candidate 1-itemsets ($C_1$)
- Filter $C_1$ to find $L_1$ based on minimum weighted support
Iterative Generation and Pruning
- While $L_{k-1}$ is not empty:
  - Generate candidate k-itemsets $C_k$ from $L_{k-1}$ using apriori_gen
  - Calculate support for candidates by intersecting K-order subset support transactions
  - Filter $C_k$ to find frequent k-itemsets $L_k$
  - Update the total frequent set $F$ and increment $k$
Return $F$

Core Optimization: Intersection-Based Counting

The algorithm’s key optimization is in Step 4, where the count of a candidate itemset $C$ is found by determining the intersection of support transactions in all K-order subset support affairs. This process makes it equivalent to finding the support $K+1$ without needing to re-scan the source database multiple times.

How It Works

For a candidate k-itemset $C$:

Generate all (k-1)-subsets of $C$
Retrieve the support transactions (transaction IDs) for each (k-1)-subset
Compute the intersection of all these support transaction sets
The size of the intersection gives the support count for $C$

Example:

For candidate itemset {A, B, C}:
- Find support transactions for {A, B}
- Find support transactions for {A, C}
- Find support transactions for {B, C}
- Intersect all three sets
- The intersection size = support count for {A, B, C}

Pseudocode

Main Algorithm

// 1. Scan DB once to find initial support transactions and C1
Scan DB;
Locate item_sup_trans; // Locate support transactions for all items
C1 = Generate_C1(DB); // Generate Candidate 1-itemsets

// 2. Filter C1 to find L1 based on minimum weighted support (wminsup)
L1 = locate_frequent_1_itemset; // Find L1 based on initial counts
F = {}; // Initialize the final set of frequent itemsets
k = 2; // Start iteration for L2

// Loop until no more frequent itemsets are found
While L_{k-1} is not empty {
    // 3. Generate Candidate k-itemsets Ck from L_{k-1}
    CK = apriori_gen(L_{k-1});

    // 4. Calculate support for candidates Ck by intersecting K-support transactions
    For all candidate itemset C ∈ CK {
        C.suptrans = SCk;

        // Find intersection of support transactions for all K-order subsets S of C
        While descending power subset S {
            C.suptrans = C.suptrans ∩ S.suptrans;
        }

        // C.count is determined by the size of the resulting intersection set
        C.count = |C.suptrans|;
    }

    // 5. Filter Ck to find frequent k-itemsets Lk based on weighted support
    L_k = {c ∈ C_k | C.count ≥ wminsup};

    // 6. Update the total frequent set F and increment k
    F = F ∪ L_k;
    k = k + 1;
}

Return F;

Function: `apriori_gen`

Function apriori_gen (L_{k-1}) {
    CK = {}; // Initialize candidate set Ck

    // Join Step
    For all itemset g1, g2 ∈ L_{k-1} do {
        if ( (g1_1 = g2_1) ^ (g1_{k-2} = g2_{k-2}) ^ (g1_{k-1} < g2_{k-1}) ) then {
            C = {g1_1, g1_2, ..., g1_{k-1}, g2_{k-1}};
            add C to CK;
        }
    }

    // Pruning Step
    For all C ∈ CK do {
        For all (K-1) itemset X ⊂ C do {
            if (X ∉ L_{k-1}) then {
                delete C from CK;
            }
        }
    }

    Return CK;
}

Implementation Structure

The ImprovedApriori class provides a complete implementation:

from improved_apriori import ImprovedApriori

model = ImprovedApriori(
    min_support=0.01,      # Minimum weighted support threshold
    min_confidence=0.5    # Minimum confidence threshold
)

model.fit(transactions)
model.generate_association_rules()

# Get results
frequent_itemsets = model.get_frequent_itemsets()
association_rules = model.get_association_rules()
runtime_stats = model.get_runtime_stats()

Key Features

1. Single Database Scan

Scans the database once to find support transactions for all items
Stores transaction IDs where each item appears
Eliminates repeated database scans

2. Intersection-Based Counting

Calculates support by intersecting (k-1)-subset support transactions
No need to rescan database for candidate itemsets
Efficient set operations for support calculation

3. Support Transaction Storage

Maintains a dictionary mapping itemsets to their support transaction sets
Enables efficient intersection operations
Supports association rule generation without database rescanning

4. Runtime Metrics

Comprehensive runtime tracking:
- fit_time: Total time for fit() method
- frequent_itemsets_time: Time to find frequent itemsets
- association_rules_time: Time to generate association rules
- initial_scan_time: Time for initial database scan
- candidate_generation_time: Total time for candidate generation
- support_calculation_time: Total time for support calculation via intersection

Performance Advantages

Compared to traditional Apriori:

Reduced Database Scans
- Traditional Apriori: Scans database once per iteration (k scans)
- Improved Apriori: Scans database only once (1 scan)
Efficient Support Calculation
- Traditional Apriori: Scans entire database for each candidate
- Improved Apriori: Uses set intersection operations on stored transaction IDs
Memory Efficiency
- Stores transaction IDs (integers) instead of full transaction data
- Set intersection operations are highly optimized in Python
Scalability
- Performance improvement increases with dataset size
- Set operations scale better than database scans

Complexity Analysis

Time Complexity:
- Database scan: O(n × m) where n = transactions, m = average items per transaction
- Candidate generation: O(|L_{k-1}|²) for join step
- Support calculation: O(k × |C_k| × avg_support_trans_size) using intersections
- Overall: Better than traditional Apriori due to single scan
Space Complexity:
- Support transactions storage: O(|F| × avg_support_size)
- Frequent itemsets: O(|F|)
- Similar to traditional Apriori

Comparison with Other Algorithms

vs. Traditional Apriori

✅ Single database scan vs. multiple scans
✅ Faster support calculation via intersection
✅ Same correctness - produces identical results
✅ Better runtime metrics for detailed analysis

vs. FP-Growth

✅ Maintains Apriori’s interpretability - candidate generation is explicit
✅ No tree construction overhead - simpler data structures
⚠️ Still generates candidates (though more efficiently)
⚠️ May generate more candidates than FP-Growth’s pattern growth approach

Current Status

The improved Apriori algorithm is:

✅ Fully implemented with intersection-based counting
✅ Comprehensive runtime tracking for performance analysis
✅ Complete association rule generation using stored support transactions
✅ Well-documented with detailed docstrings and comments
✅ Production-ready for use in frequent itemset mining

Usage Example

from improved_apriori import ImprovedApriori

# Prepare transactions
transactions = [
    ['bread', 'milk'],
    ['bread', 'diaper', 'beer', 'eggs'],
    ['milk', 'diaper', 'beer', 'cola'],
    ['bread', 'milk', 'diaper', 'beer'],
    ['bread', 'milk', 'diaper', 'cola']
]

# Initialize and run algorithm
model = ImprovedApriori(min_support=0.6, min_confidence=0.5)
model.fit(transactions)
model.generate_association_rules()

# Get results
frequent_itemsets = model.get_frequent_itemsets()
association_rules = model.get_association_rules()
runtime_stats = model.get_runtime_stats()

# Display results
print("Frequent Itemsets:")
for size, itemsets in frequent_itemsets.items():
    print(f"{size}-itemsets: {len(itemsets)}")

print(f"\nAssociation Rules: {len(association_rules)}")
print(f"\nRuntime Statistics:")
for metric, value in runtime_stats.items():
    print(f"  {metric}: {value:.4f}s")

Experimental Results

Our implementation includes comprehensive runtime tracking and visualization. See the Results page for detailed performance analysis and comparison with Traditional Apriori and FP-Growth.

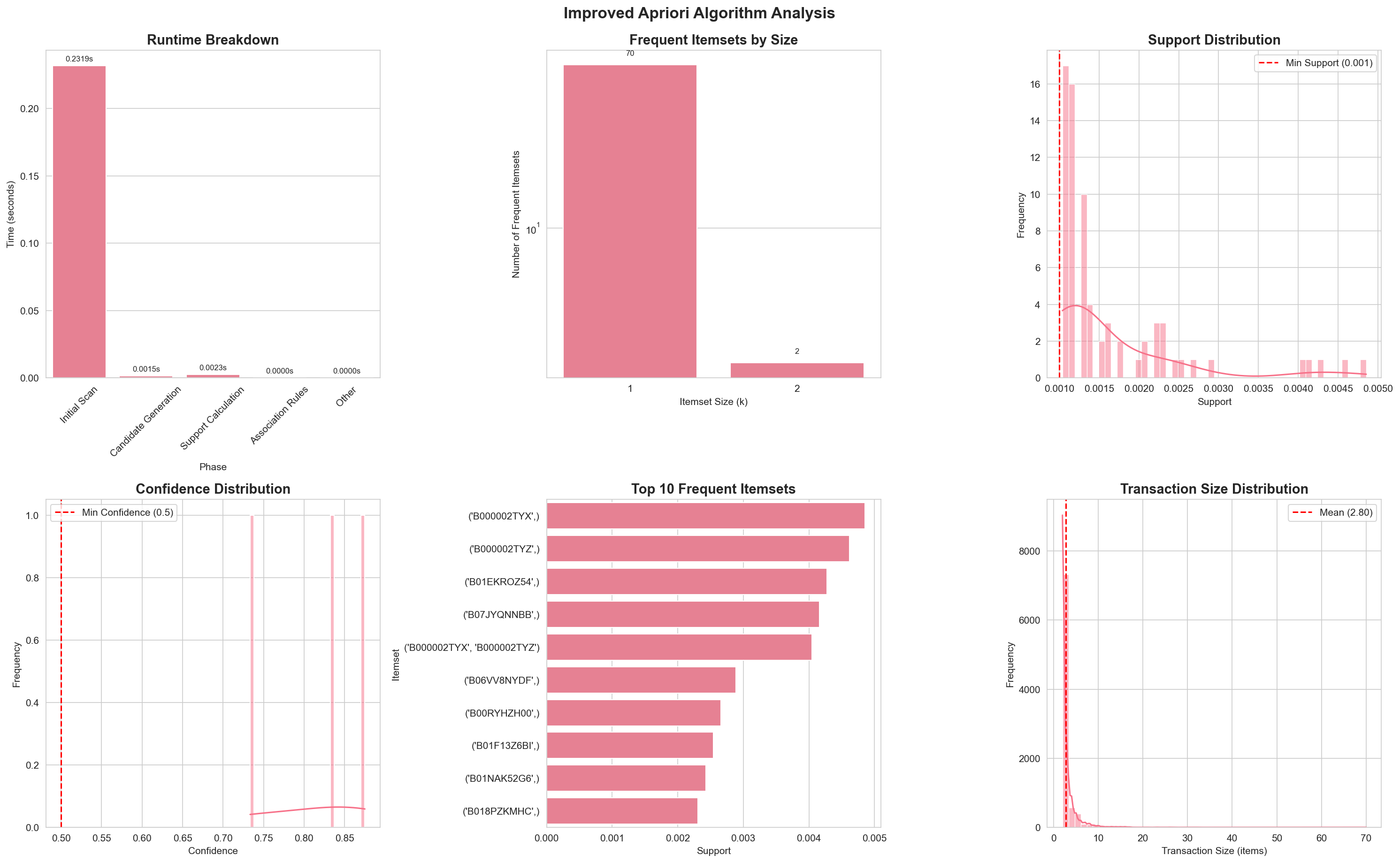
Improved Apriori Algorithm Analysis

Complete analysis visualization showing detailed runtime breakdown (initial scan, candidate generation, support calculation), frequent itemsets by size, support and confidence distributions, top itemsets, and transaction size distribution.

The Improved Apriori algorithm demonstrates:

~10x speedup over traditional Apriori through single database scan optimization
Identical results to traditional Apriori, validating correctness
Detailed runtime metrics showing the effectiveness of intersection-based counting
Consistent performance across different support thresholds

Traditional Apriori Algorithm - Standard implementation with multiple database scans
FP-Growth Algorithm - Tree-based approach avoiding candidate generation

Improved Apriori Algorithm